Day 18 - Dot Product

The Dot Product of two vectors is defined by summing the products of their corresponding components.

$$v\cdot w = v_{1}w_{1} + v_{2}w_{2} + \cdots$$

The result of the dot product between a vector and itself is equal to the square of its magnitude.

$$v\cdot v = {v_{1}}^{2} + {v_{2}}^{2} + \cdots = \|v\|^2$$

---

If the vectors $v$ and $w$ are perpendicular, their magnitudes satisfy the Pythagorean Theorem when added together:

$$\|v+w\|^{2} = \|v\|^{2} + \|w\|^{2}$$

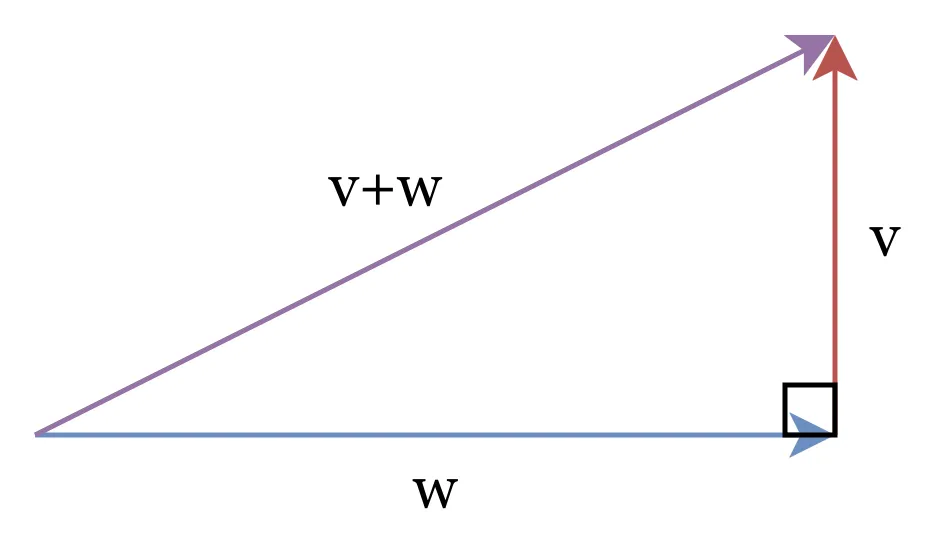
We also can rewrite this equation through the expansion of the squared magnitude of $v + w$:

$$\begin{aligned} \|v+w\|^{2} &= (v_{1}+ w_{1})^{2} + (v_{2}+w_{2})^{2} + \cdots\\ &= ({v_{1}}^{2} + 2v_{1}w_{1} + {w_{1}}^{2}) + ({v_{2}}^{2} + 2v_{2}w_{2} + {w_{2}}^{2}) + \cdots\\ &= ({v_{1}}^{2} + {v_{2}}^{2} + \cdots)+ 2(v_{1}w_{1} + v_{2}w_{2} + \cdots) + ({w_{1}}^{2} + {w_{2}}^{2} + \cdots) \\ &= v \cdot v + 2(v \cdot w) + w\cdot w \end{aligned}$$

Replacing each dot product with its corresponding magnitude gives:

$$\|v+w\|^{2} = \|v\|^{2} +2(v\cdot w) + \|w\|^ {2}$$

Comparing this expression with the Pythagorean identity shows that:

$$v\cdot w = 0$$

when $v$ and $w$ are perpendicular.

---

Now consider the case where both $v$ and $w$ are unit vectors, and let $\theta$ denote the angle between two vectors.

By rotating the coordinate system so that $w$ lies along the positive $x$-axis, we may express $w$ as:

$$w = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$$

while $v$ can be expressed as:

$$v = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix}$$

Taking the dot product between the two vectors yields:

$$v\cdot w = \cos\theta$$

This result can be extended to non-unit vectors by normalizing both vectors first.

$$\left(\frac{v}{\|v\|}\right)\cdot\left(\frac{w}{\|w\|}\right) = \cos\theta$$

Multiplying both sides by $\|v\| \|w\|$ leads to the general dot product formula:

$$v \cdot w = \|v\|\|w\|\cos\theta$$

---

• Strang, Gilbert. Introduction to Linear Algebra. 5th ed. Wellesley–Cambridge Press, 2016. Chapter 1.2.