Day 17 - Markov Chains

we're running it back.
26 Dec 2025

Merry Christmas. I haven’t worked on this project in a while, but I think it is time to resume it.

Nearing the Russian Revolution, mathematician Andrey Markov developed a method to study sequences of dependent random events. To test his ideas, he analyzed the distribution of vowels and consonants in Eugene Onegin, treating each letter as a separate state. Remarkably, he showed that these sequences still adhered to the law of large numbers and the central limit theorem.

This approach led to the concept now known as a Markov Chain, a system that models a sequence of possible events in which the probability of each event depends only on the immediately preceding event.

A Weather Example

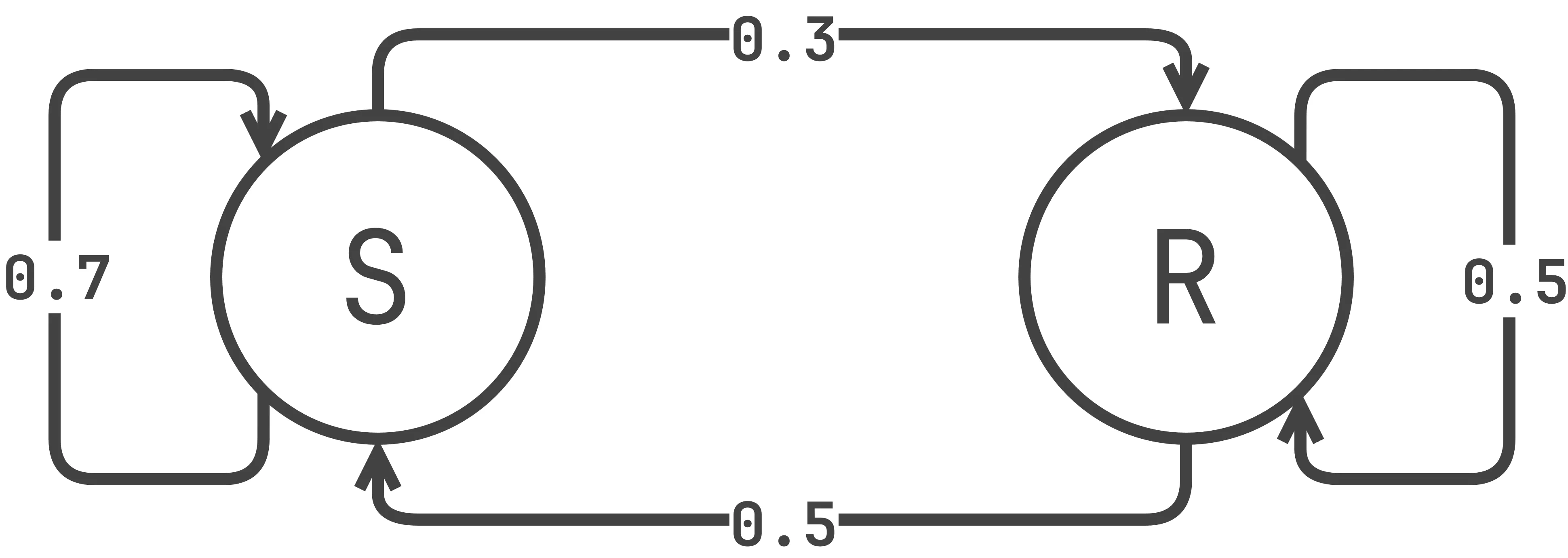
Consider a simple weather model, where each day can be either Sunny or Rainy. The probability of tomorrow’s weather depends only on today’s weather:

  • If today is sunny, there is a 70% chance it stays sunny and a 30% chance it rains tomorrow.

  • If today is rainy, there is a 50% chance it continues raining and a 50% chance of sun.

We can represent this scenario using the following Markov Chain equations:

πS=0.7πS+0.5πR \pi_{S} = 0.7 \pi_{S} + 0.5 \pi_{R} πR=0.3πS+0.5πR \pi_{R} = 0.3 \pi_{S} + 0.5 \pi_{R}

We can then illustrate the Markov Chain as a diagram:

Markov Chain.

Transition Matrix

A Markov Chain can also be represented as a Transition Matrix.

P=[P(S→S)P(S→R)P(R→S)P(R→R)]=[0.70.30.50.5]P = \begin{bmatrix} P(S \to S) & P(S \to R) \\ P(R \to S) & P(R \to R) \end{bmatrix} = \begin{bmatrix} 0.7 & 0.3 \\ 0.5 & 0.5 \end{bmatrix}

Here, each row represents the current state, each column represents the next state, and each entry indicates the probability of that transition.

By iterating through the model step by step, starting from an initial state, the next state is chosen according to the transition probabilities. Repeating this process allows us to generate sequences of events. Over time, the system tends toward a steady-state distribution, where the probability of being in each state stabilizes.

This steady-state vector π\pi satisfies the following equations:

πP=π,πS+πR=1 \pi P = \pi, \quad \pi_{S} + \pi_{R} = 1

Solving these equations, we find that:

πS=58=0.625,πR=38=0.375 \pi_{S} = \frac{5}{8} = 0.625, \quad \pi_{R} = \frac{3}{8} = 0.375

We can check this by simulating the chain using this python code:

import numpy as np

# Transition matrix
P = np.array([[0.7, 0.3],
              [0.5, 0.5]])

# Initial state (Sunny, Rainy)
state = np.array([1.0, 0.0])

# Iterate many times
for _ in range(1000):
    state = state @ P  # Multiply current state by transition matrix

print("Approximate steady-state distribution:")
print(f"Sunny: {state[0]:.3f}, Rainy: {state[1]:.3f}")

Applications

Markov Chains are used everywhere, like in search engines, for example, which rely on them to rank webpages by estimating the likelihood that a user will follow links from one page to another, forming the basis of algorithms such as Google’s PageRank.

Another use case of Markov models is with predictive text systems, by anticipating the next word based on the previous one.